Training Neural Networks using Fomoh

This blog post focuses on training neural networks using the Fomoh library. Fomoh has a direct interface with PyTorch. We will see how to pass weights between PyTorch modules and Fomoh Models. This tutorial also shows you how to train a simple neural network.

For those of you looking for an introduction into how to use Fomoh, please refer to my previous post. The code for this blog post can be found here.

Fomoh: Models and Layers

To start this tutorial, we will focus on the structure of a fully-connected neural network and introduce some of the key methods and attributes of the Fomoh model base class, Model. In the current version of Fomoh, we can import models such as DenseModel and CNNModel directly. However, building new ones requires a basic understanding of how these models are structured.

The first line of code in our tutorial is given by the simple Python imports:

import torch
from fomoh.hyperdual import HyperTensor as htorch
from fomoh.nn import DenseModel, nll_loss
from fomoh.nn_models_torch import DenseModel_Torch
from tqdm.notebook import tqdm
import matplotlib.pyplot as plt

Some key things to note:

• As is customary, we import the Fomoh HyperTensor as htorch.
• Fomoh neural network models are in the fomoh.nn.
• Equivalent PyTorch models are in fomoh.nn_models_torch.

Fully-Connected Neural Network Example

The DenseModel is defined in the in the nn.py file:

# fomoh/nn.py
from fomoh.layers import Linear # Import fomoh linear layer

class DenseModel(Model): # Inherits from the Model base class
    def __init__(self, layers = [1,100,1], bias = True):
        super(DenseModel, self).__init__()
        self.layers = layers
        self.bias = bias
        self.linear_layers = []
        for n in range(len(self.layers)-1):
            # Use the base class __setattr__ to initialise a named linear layer
            if self.bias:
                self.__setattr__(f'linear_{n+1}', Linear(self.layers[n], self.layers[n+1], bias, names = [f'W{n+1}', f'b{n+1}']))
            else:
                self.__setattr__(f'linear_{n+1}', Linear(self.layers[n], self.layers[n+1], bias, names = [f'W{n+1}']))
            # Gather all the layers in a list for ease of use
            self.linear_layers.append(getattr(self, f'linear_{n+1}'))
        self.n_params = self.count_n_params() # Count number of params

    # Equivalent to forward function for torch.nn.module  
    def __call__(self, x, v1, v2=None, requires_grad=False):
        """
        x:  input to model, type: htorch, Batch x Dim
        v1: parameter tangent vector corresponding to eps1, type: list of torch.tensors of shape of the params
        v2: same as v1 if set to None, else corresponds to a different eps2
        requires_grad: set to False unless there is a need to differentiate through using torch.autograd
        """
        if v1 is None:
            # Simple forward pass, with no forward-mode AD
            v1 = [None for _ in self.params]
            v2 = [None for _ in self.params]
        elif v2 is None:
            v2 = v1
        # Use the base class convert_params_to_htorch to prepare params
        # Consider this step equivalent to fomoh's equivalent of requires_grad
        params = self.convert_params_to_htorch(v1, v2, requires_grad=requires_grad)
        
        # Keep track of the index of params, i
        i = 0
        for n in range(len(self.layers)-1):
            x, i = self.linear_layers[n](x, params, i)
            if n < ( len(self.layers) - 2):
                x = x.relu()
        return x

Above, we see that Fomoh models inherit from the fomoh.nn.Model base class. The base class has many useful default methods which we will come across in this tutorial. For example, we see these functions used in the initialization¹ of the model in the form of self.__setattr__ and self.count_n_params(), as well as in the forward part of the model, in the form of self.convert_params_to_htorch.

• self.__setattr__ automatically adds parameters to the model when it sees a fomoh.layers.Layer object.
• self.count_n_params() is also called every time we add parameters.
• self.convert_params_to_htorch is vital to setting up the forward-mode Fomoh backend. It attaches the tangent vectors v1 and v2 to their corresponding parameters in the model.

Additional Requirements: We must use layers defined in fomoh.layers and keep track of the index of the parameters in the __call__ method.

Comparison between Fomoh and PyTorch

In our notebook example, the first interesting part of the Fomoh library to explore is comparing forward passes and gradients to PyTorch. This should give us confidence that everything is working properly. It also introduces enough details to start building a training loop later on.

First, let’s initialize the Fomoh model as hmodel and PyTorch model as tmodel. We will use h and t to distinguish between the two comparable set-ups.

device = "cpu"
hmodel = DenseModel(layers = [784,100,10])
tmodel = DenseModel_Torch(layers=[784,100,10])
# Map torch weights to fomoh model weights:
hmodel.nn_module_to_htorch_model(tmodel)
hmodel.to(device)

Here, we come across two more in-built Model methods. First nn_module_to_htorch_model, takes the PyTorch model and copies the initialized weights to the hmodel. Second, we see the familiar to, which puts the hmodel onto the "cpu" (feel free to switch this to a GPU).

Now that we have initialized both models with the same weights, let’s focus on getting everything we need from the PyTorch model. We want to compare to: the output, the first derivative, and the second derivative. The only atypical line in the code below is that we include create_graph=True in the backward, due to our desire to compare to the second derivative. Otherwise, this code should look familiar to a seasoned PyTorch user:

# Zero out grads just in case:
for p in tmodel.parameters():
    p.grad = None
crit = torch.nn.CrossEntropyLoss()
tdata = torch.randn(10,784)
tlabels = torch.randint(0,10,(10,))
tpred = tmodel(tdata)
tloss = crit(tpred, tlabels)
tloss.backward(create_graph=True) # This might raise a warning but don't worry

For the hmodel, we get to the hloss following the same structure, with the addition of defining a tangent vector, v, and converting the data and labels to the htorch tensors. The method, vec_to_params, reshapes a flat vector to the parameter shape of the model. This is required before using the model as a callable.

loss_module = lambda x, y: nll_loss(x.logsoftmax(-1), y)
v_flat = torch.randn(hmodel.n_params)
v = hmodel.vec_to_params(v_flat) # define tangent vector and reshape to params list
hdata = htorch(tdata)
hlabels = htorch(tlabels)
hpred = hmodel(hdata, v)
hloss = loss_module(hpred, hlabels)

Check simple forward passes match:

We can check that both models behave the same prior to analysing the gradients:

print("Predictions match: ", torch.allclose(hpred.real, tpred, rtol = 1e-7, atol = 1e-7))
print("Losses match: ", torch.allclose(hloss.real, tloss, rtol = 1e-7, atol = 1e-7))

Predictions match:  True
Losses match:  True

Check directional derivatives match:

To check whether the directional derivatives match, we just need to collect the gradients from PyTorch’s reverse-mode automatic differentation (backpropagation) and perform a dot product with the tangent vector v. This should be the same as the hloss.eps1 component calculated through forward-mode automatic differentation using Fomoh. (Note that in this case it would also equal hloss.eps2 as v1 = v2.)

# Collect torch grads: (using in-build Model function)
grads_p_shape = hmodel.collect_nn_module_grads(tmodel)
# Convert to flat vector
grads = hmodel.params_to_vec(grads_p_shape)
print("Directional derivatives match: ", torch.allclose(hloss.eps1, grads @ v_flat, rtol = 1e-5, atol = 1e-5))

Directional derivatives match:  True

Check quadratic second-order term matches:

The final component to check is the second-order component of the hloss, i.e. hloss.eps1eps2 or \(\mathbf{v}^{\top}\mathbf{H}\mathbf{v}\). A simple way to get this second-order term with PyTorch is to evaluate the Hessian-vector-product (HVP) and dot the result with the tangent vector. The following code does this, with the only complicated part ensuring that everything is the right shape, and the right layers in the model are dotted with the right part of the tangent vector:

# Use Hessian vector product to check second order matches:
reshape = lambda x : [v_.t() if len(v_.shape) == 2 else v_ for v_ in x] # function to transpose the correct weights
Hv = torch.autograd.grad(reshape(grads_p_shape), tmodel.parameters(), grad_outputs=reshape(v), only_inputs=True)
vTHv = sum((v_.flatten().dot(hv.flatten().detach()) for v_, hv in zip(reshape(v), Hv)))

print("Quadratic terms match (v^T H v): ", torch.allclose(hloss.eps1eps2, vTHv, rtol = 1e-5, atol = 1e-5))

Quadratic terms match (v^T H v):  True

Neural Network Optimization with FoMoH-KD

We now demonstrate how to optimize a Fomoh neural network model using FoMoH-KD. This is the optimization approach of our paper “Second-Order Forward-Mode Automatic Differentiation for Optimization” that we went over in the previous tutorial.

The main function that performs the update step is fomoh.opt.optimizer_step_plane_Nd. This function takes in the following arguments:

• model: This is any model inheriting from the fomoh.nn.Model that follows the same structure as our hmodel from this tutorial.
• loss_module: This is the loss function handle that expects the model prediction and the labelled data as an input. In this tutorial we use loss_module = lambda x, y: nll_loss(x.logsoftmax(-1), y).
• n_sample_directions: This argument controls the number of times to sample the tangent vectors over which to average. We set this to 1 to follow the standard implementation from our paper.
• inputs: This is just the input to the model. In the above Fomoh, PyTorch comparison example, this would be tdata since the function converts to it to a Fomoh hyper-dual tensor internally.
• labels: This is the PyTorch tensor of labels corresponding to tlabels above.
• N: This corresponds to the K in FoMoH-KD, which is the dimension of the hyperplane step.
• device: Device to run on. Default is "cpu" in this example but it runs faster and more efficiently on the GPU.
• clip_value: When updating the weights at each step, this controls the absolute largest allowed update. Setting to 0.0 switches this off. We will do that here.
• lr: Learning rate.
• vectorized: Controls whether to run multiple forward passes in parallel. We will directly explore this in the last part of this tutorial.

Having explained this function, we can write the code that incorporates the FoMoH-KD step. This code should look similar to writing normal training and validation steps, where the less interesting code of the train_loader and test_loader are defined in the notebook:

from fomoh.opt import optimizer_step_plane_Nd

def train_step(train_loader, model, loss_module, number_hyperplane_directions, lr, vectorized = False):
    model.train() # Make sure to do this when the model includes dropout etc.
    loss = 0
    correct = 0
    for inputs, labels in train_loader:
        inputs = inputs.to(device).view(-1,28*28)
        labels = labels.to(device)
        ls, pred = optimizer_step_plane_Nd(model, loss_module, n_sample_directions=1,
                                  inputs=inputs, labels=labels, device=device, N=number_hyperplane_directions,
                                  clip_value=0.0, lr = lr, vectorized = vectorized)
        loss += labels.shape[0] * ls.real.item()
        correct += sum(torch.softmax(pred, -1).argmax(1).cpu() == labels.real.cpu())
    return loss/len(train_loader.dataset), correct/len(train_loader.dataset)

def val_step(test_loader, model, loss_module):
    model.eval() # Make sure to do this when the model includes dropout etc.
    val_loss = 0
    correct = 0
    for inputs, labels in test_loader:
        inputs = htorch(inputs.view(-1,28*28).to(device))
        labels = htorch(labels.to(device))
        pred = model(inputs, None)
        l = loss_module(pred,labels)
        val_loss += l.real.cpu().item() * labels.real.shape[0]
        correct += sum(pred.logsoftmax(-1).exp().real.argmax(1).cpu() == labels.real.cpu())
    return val_loss/len(test_loader.dataset), correct/len(test_loader.dataset)

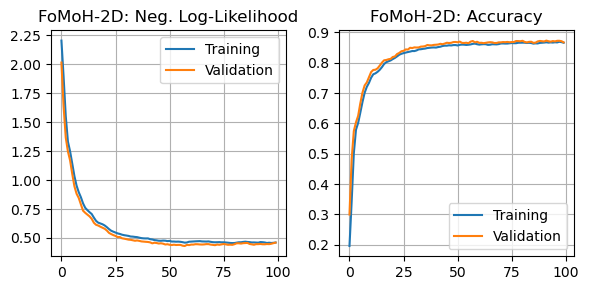
We can then run the training loop:

number_hyperplane_directions = 2
lr = 0.8
epochs = 100
loss_list = []; train_accuracy = []
val_loss_list = []; val_accuracy = []
tepoch = tqdm(range(epochs))
for i in tepoch:
    loss, correct = train_step(train_loader, hmodel, loss_module, number_hyperplane_directions, lr)
    val_loss, val_correct = val_step(test_loader, hmodel, loss_module)
    loss_list.append(loss); train_accuracy.append(correct)
    val_loss_list.append(val_loss); val_accuracy.append(val_correct)
    tepoch.set_postfix(loss=loss, val_loss = val_loss)

Parallel Implementation

Since the majority of the computations of the Fomoh backend for neural networks is matrix multiplication, I wanted to build in the possibility of being able to evaluate multiple tangents at the same time to speed up forward passes. We can simply set vectorized = True in the optimizer_step_plane_Nd to run multiple tangent vectors in one call. We can then benchmark the wall clock time of the sequential versus vectorized implementation. This is even faster on a GPU, but I have kept it on the CPU in this example to be consistent:

device = "cpu"

hmodel = DenseModel(layers = [784,100,10])
tmodel = DenseModel_Torch(layers=[784,100,10])

# map torch weights to fomoh model weights:
hmodel.nn_module_to_htorch_model(tmodel)
hmodel.to(device)

number_hyperplane_directions = 10 # Note I have increased this to FoMoH-10D
lr = 0.8

fun = lambda vectorized: train_step(train_loader, hmodel, loss_module, number_hyperplane_directions, 
                                    lr, vectorized=vectorized)

The function fun now requires the evaluation of \(55\) tangent vectors for a single step \(((K^2 + K)/2)\). We can run this as a sequential implementation:

%%timeit
# One iteration through the training loader sequential
fun(False)

14.9 s ± 456 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

Or as a vectorized implementation:

%%timeit
# One iteration through the training loader vectorized
fun(True)

8.92 s ± 123 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

This gives us a significant speed-up.

Summary

We went through how to train a neural network with Fomoh. The code is available in full here. More technical details can be seen in the paper. I hope to add more models as I extend on the current library. Please reach out if you have any questions!

Acknowledgements

This material is based upon work supported by the United States Air Force and DARPA under Contract No. FA8750-23-C-0519. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the United States Air Force and DARPA.